A simplified gravitational reference sensor for satellite geodesy

Abstract

A simplified gravitational reference sensor (S-GRS) is an ultra-precise inertial sensor for future Earth geodesy missions. These sensors measure or compensate for all non-gravitational accelerations of the host spacecraft to remove them in the data analysis and recover spacecraft motion due to Earth’s gravity field. Low–low satellite-to-satellite tracking missions like GRACE-FO that use laser ranging interferometers (LRI) are limited by the acceleration noise performance of their electrostatic accelerometers and temporal aliasing associated with Earth’s gravity field. The current accelerometers, used in the GRACE missions, have a limited sensitivity of $\sim \,10^{-10}$ m/s$^{2}$/Hz$^{1/2}$ around 1 mHz. The S-GRS is estimated to be at least 40 times more sensitive than the GRACE accelerometers and over 500 times more sensitive if operated on a drag-compensated platform. This improvement is enabled by increasing the mass of the sensor’s test mass, increasing the gap between the test mass and its electrode housing, removing the grounding wire used in GRACE, and replacing it with a UV LED-based charge management system. This allows future missions to take advantage of the sensitivity of the GRACE-FO LRI in the gravity recovery analysis. The S-GRS concept is a simplified version of the flight-proven LISA Pathfinder (LPF) GRS. Performance estimates are based on models vetted during the LPF flight and the expected spacecraft environment based on GRACE-FO data. The relatively low volume ($\sim \,10^4$ cm$^3$), mass ($\sim$ 13 kg), and power ($\sim$ 20 W) enable the use of S-GRS on microsatellites, reducing launch costs and allowing more satellite pairs to improve the temporal resolution of gravity field maps. The S-GRS design and analysis, as well as its gravity recovery performance in two candidate mission architectures, are discussed in this article.

Appendices

Appendix A: Models for performance estimates

High-fidelity numerical simulations relying on the same software suite used to process GRACE and GRACE-FO data at JPL were run to quantify performance in Figs. 1 and 2. The simulations consist of a truth run to create a set of synthetic satellite observations based on a realistic flight environment, followed by a nominal run where the truth measurements are perturbed in some way. The error in the recovered gravity field due to this perturbation is then quantified via a large linear least squares estimation process, as is commonly used in the GRACE and GRACE-FO data processing. Force models used in the truth and nominal runs are given in Table 2 when temporal aliasing error is included in the simulation. When only measurement system error is considered, the nominal models in Table 2 are set equivalent to the truth models, so there is no perturbation among the model. The simulation timeframe is January 1–29, 2006. The gravity estimation process is a 2-step process, where in the first step, a set of “local” parameters are estimated using the tracking data to converge to the best fitting orbit. These parameters consist of daily position and velocity of each spacecraft, daily accelerometer scale factors and biases, and range-rate biases, drifts, and one cycle per revolution each orbital revolution. In the second step of the gravity estimation process, these same parameters are again adjusted along with a 29-day mean gravity field expressed to spherical harmonic degree and order 180. A diagonal weighting matrix is used for the tracking observations (LRI range-rate and kinematic orbits); and relative weights between the two data types are estimated in an optimal fashion as described in Section 3.4 of Watkins et al. (2015).

Table 4 Table of abbreviations

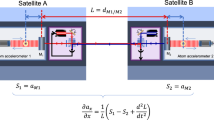
Measurement system errors ingested into the simulation process rely largely on heritage information from GRACE-FO. Orbit error is introduced by adding white noise with a 1 cm standard deviation in all 3-axes with a 5-min sampling time. Attitude Error is derived using the difference of two competing data products used to define the GRACE-FO attitude. For pitch and yaw, the difference between an attitude solution that combines star tracker and IMU data (as in the GRACE-FO v04 SCA1B data product) with star tracker and laser steering mirror data (from the LRI) is used to define the error (Goswami et al. 2021). Since the laser steering mirror is insensitive to roll variations, roll error is defined as the difference between an attitude solution that uses only star tracker data with one that uses both star tracker and IMU data. LRI error is derived from GRACE-FO flight data (Abich et al. 2019), where laser frequency noise dominates high frequencies and tilt-to-length coupling error dominates lower frequencies (Wegener et al. 2020). The LRI error curves with “improved alignment” assume the tilt-to-length coupling error is driven to zero via improved alignments relative to the center of mass of the spacecraft. The GRACE-FO accelerometer error is taken as the best estimate of performance prior to launch of GRACE-FO and is approximately a factor 3 better than the requirement discussed in Kornfeld et al. (2019). The S-GRS error is described in detail in Sect. 4. Satellites have a separation distance of 300 km.

Many previous studies have compared single and dual-pair architectures for recovering time variations in the Earth’s gravity field. While differences in simulation setups across studies make it difficult to compare results at a granular level, results can be compared on a macro level. We note that the simulation results we show (relative improvement of dual-pair over single pair, and relative contribution of different measurement system components to the overall error budget) agree with previously published studies at the macro scale (Wiese et al. 2011b; Purkhauser et al. 2020; Hauk and Wiese 2020).

Appendix B: Technology readiness level

Projects are classified depending on the level of maturity of their technology through a system called the Technology Readiness Level (TRL) (NASA 2010). The system uses a numeric scale that starts at 1 for “reporting and observation of basic principles” and ends at 9 for flight-proven technology. For a technology to be included into a new mission, it must progress through the TRL scale until it is flight ready (TRL 8). Table 3 shows the current and goal TRL values for the S-GRS head, the caging mechanism, and CMS.

Appendix C: Abbreviations

See Table 4.